1. 多模匹配
AC自动机(Aho-Corasick Automaton)是多模匹配算法的一种。所谓多模匹配,是指在字符串匹配中,模式串有多个。前面所介绍的、为单模匹配,即模式串只有一个。假设主串\(T[1 \cdots m]\),模式串有k个\(\mathbb{P} = \{ P_1, \cdots, P_k\}\),且模式串集合的总长度为\(n\)。如果采用KMP来匹配多模式串,则算法复杂度为:
\[ O(|P_1|+m+\cdots + |P_k|+m)=O(n+km) \]
而KMP并没有利用到模式串之间的重复字符结构信息,每一次的匹配都需要将主串从头至尾扫描一遍。贝尔实验室的Aho与Corasick于1975年基于有限状态机(finite state machines)提出AC自动机算法[1]。小插曲:实际上AC算法比KMP提出要早,KMP是1977年才被提出来了的。
2. AC算法
AC自动机
自动机由状态(数字标记的圆圈)和转换(带标签的箭头)组成,每一次转换对应一个字符。AC算法的核心包括三个函数:goto、failure、output;这三个函数构成了AC自动机。对于模式串{he, his, hers, she},goto函数表示字符按模式串的转移,暗含了模式串的共同前缀的字符结构信息,如下图:
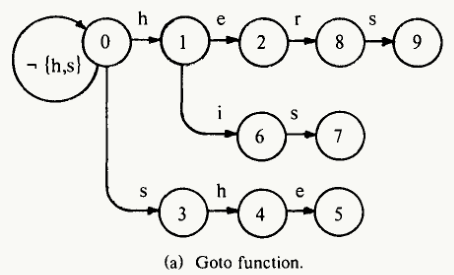
failure函数表示匹配失败时退回的状态:

output函数表示模式串对应于自动机的状态:

完整的AC自动机如下:

匹配
AC算法根据自动机匹配模式串,过程比较简单:从主串的首字符、自动机的初始状态0开始,
- 若字符匹配成功,则按自动机的goto函数转移到下一状态;且若转移的状态对应有output函数,则输出已匹配上的模式串;
- 若字符匹配失败,则递归地按自动机的failure函数进行转移
匹配母串的算法如下:

构造
AC自动机的确简单高效,但是如何构造其对应的goto、failure、output函数呢?首先来看goto函数,细心一点我们发现goto函数本质上就是一棵带有回退指针的trie树,利用模式串的共同前缀信息,与output函数共同表示模式串的字符结构的信息。
failure函数是整个AC算法的精妙之处,用于匹配失败时的回溯;且回溯到的状态\(state\)应满足:状态\(state\)能按当前状态的转移字符进行能goto到的状态,且能构成最长匹配。记\(g(r,a)=s\)表示状态r可以按字符a goto到状态s,则称状态r为状态s的前一状态,字符a为状态s的转移字符。failure函数满足这样一个规律:当匹配失败时,回溯到的状态为前一状态的failure函数值(我们称之为failure转移状态)按转移字符能goto到的状态;若不能,则为前一状态的failure转移状态的failure转移状态按转移能goto到的状态;若不能,则为......上面的话听着有点拗口,让我们以上图AC自动机为例子来说明:
- 对于状态7,前一状态6的failure转移状态为0,状态0按转移字符s可以goto到状态3,所以状态7的failure函数\(f(7)=3\);
- 对于状态2,前一状态1的failure转移状态为0,状态0按转移字符e可以goto到状态0,所以状态2的failure函数\(f(2)=0\);
其中,所有root节点(状态0)能goto到的状态,其failure函数值均为0。根据goto表(trie树)的特性,可知某一状态的前一状态、转移字符是唯一确定的。因此定义\(\beta(s)=r\)表示状态\(s\)的前一状态为\(r\),\(\tau(s)=a\)指状态\(s\)的转移字符为\(a\);记\(f^{i}(s)=f\left( f^{(i-1)}(s)\right)\)。那么,状态s的failure函数的计算公式为:
\[ f(s) = \left\{ {\matrix{ {g\left( f^{n}(\beta(s)), \tau(s) \right)} & n = \arg \underset{i}{\min} \, \left\{ g\left( f^{i}(\beta(s)), \tau(s) \right) \neq failure \right\}\cr {0} & else \cr } } \right. \]
在计算failure函数时,巧妙地运用队列进行递归构造,具体实现如下:

3. 实现
Talk is cheap, show me the code. Java版实现在;下面给出python实现(代码参考了 ):
# coding=utf-8from collections import deque, namedtupleautomaton = []# state_id: int, value: char, goto: dict, failure: int, output: setNode = namedtuple("Node", "state value goto failure output")def init_trie(words): """ creates an AC automaton, firstly create an empty trie, then add words to the trie and sets fail transitions """ create_empty_trie() map(add_word, words) set_fail_transitions()def create_empty_trie(): """ initialize the root of the trie """ automaton.append(Node(0, '', {}, 0, set()))def add_word(word): """add word into trie""" node = automaton[0] for char in word: # char is not in trie if goto_state(node, char) is None: next_state = len(automaton) node.goto[char] = next_state # modify goto(state, char) automaton.append(Node(next_state, char, {}, 0, set())) node = automaton[next_state] else: node = automaton[goto_state(node, char)] node.output.add(word)def goto_state(node, char): """goto function""" if char in node.goto: return node.goto[char] else: return Nonedef set_fail_transitions(): """construction of failure function, and update the output function""" queue = deque() # initialization for char in automaton[0].goto: s = automaton[0].goto[char] queue.append(s) automaton[s] = automaton[s]._replace(failure=0) while queue: r = queue.popleft() node = automaton[r] for a in node.goto: s = node.goto[a] queue.append(s) state = node.failure # failure transition recursively while goto_state(automaton[state], a) is None and state != 0: state = automaton[state].failure # except the chars in goto function, all chars transition will goto root node self if state == 0 and goto_state(automaton[state], a) is None: goto_a = 0 else: goto_a = automaton[state].goto[a] automaton[s] = automaton[s]._replace(failure=goto_a) fs = automaton[s].failure automaton[s].output.update(automaton[fs].output)def search_result(strings): """AC pattern matching machine""" result_set = set() node = automaton[0] for char in strings: while goto_state(node, char) is None and node.state != 0: node = automaton[node.failure] if node.state == 0 and goto_state(node, char) is None: node = automaton[0] else: node = automaton[goto_state(node, char)] if len(node.output) >= 1: result_set.update(node.output) return result_setinit_trie(['he', 'she', 'his', 'hers'])print search_result("ushersm") -------------------------------------------------------- 2016-06-14 更新 --------------------------------------------------------
实现了一个scala版本,支持添加词属性,代码托管在。4. 参考资料
[1] Aho, Alfred V., and Margaret J. Corasick. "Efficient string matching: an aid to bibliographic search." Communications of the ACM 18.6 (1975): 333-340.
[2] Pekka Kilpeläinen, .